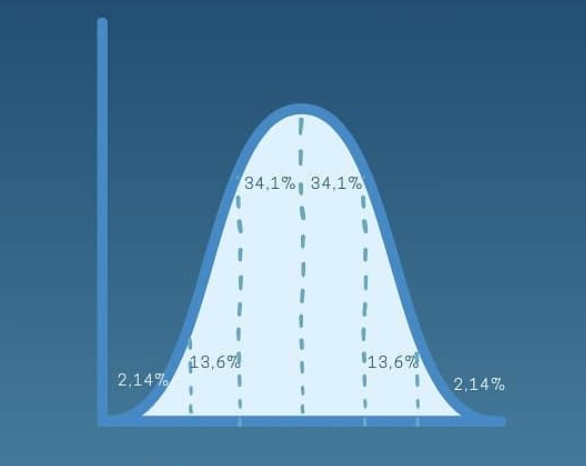
O teorema do limite central nos diz que independentemente da distribuição de uma amostra, as médias de várias amostras de uma mesma população, quando agrupadas, terão distribuição normal.

Distribuição normal.
Com esse teorema poderemos estimar distribuição populacional de algum parâmetro baseado em somente uma amostra. E assim podemos determinar se algum paciente nosso fica próximo ou longe da média populacional. Esse é o raciocínio dos escores-Z que se tem na caderneta da criança em pediatria (curvas de peso para idade, etc.)
Normalmente a média da amostra que coletamos é o melhor estimativa da média populacional que temos. No entanto devemos calcular o Intervalo de Confiança da população para saber em qual intervalo realmente se encontra a média populacional. Esse cálculo se dá por:
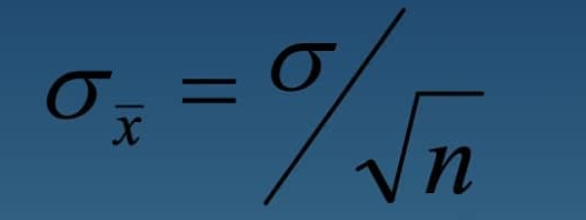
Esse cálculo se dá por: onde sigmax é o erro padrão da população , sigma é o desvio padrão da amostra e n é o tamanho da amostra em que nos baseamos. O intervalo de confiança em uma amostra normal está a + ou — 1.96 Erros Padrão da média.
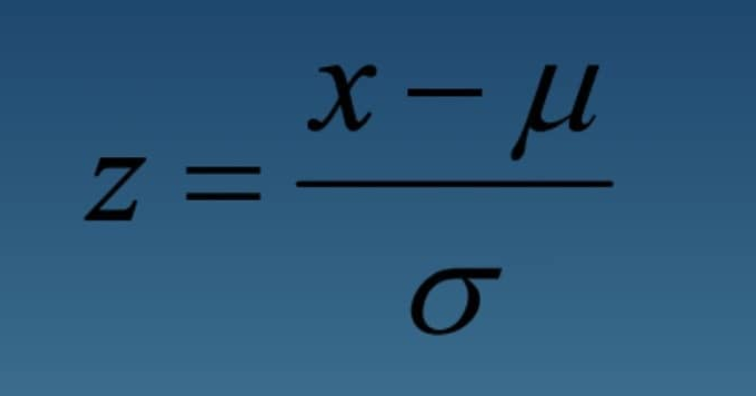
Onde x é o parâmetro de um indivíduo e u a média populacional e sigma o erro padrão daquela população
Agora segundo o teorema do Limite central sabemos que 95% da nossa população deve se encontrar entre 2 erros padrões da média estimada(para cálculos com base em amostras com n< 60, utilizar a tabela de distribuição-t para o cálculo do IC95%).